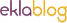-
Calcul et problèmes
C3: LA MULTIPLICATION POSEE
Effectuer des multiplications posées
C5: LA DIVISION POSEE
Exercice division assistée (division à un chiffre)
Division posée: diviseur à un chiffre
C6: LA DIVISION POSEE (2)
La division est l’opération inverse de la multiplication.
Ex : 3 x 5 = 15 alors 15 : 3 = 5 et 15 : 5 = 3
La division est un partage. Elle permet de connaître :
- le nombre de parts
- la valeur d’une part
VOCABULAIRE & TECHNIQUE DE LA DIVISION
Effectuer une division, c’est effectuer en réalité une succession de petites divisions.
LE RESTE DOIT TOUJOURS ÊTRE PLUS PETIT QUE LE DIVISEUR !!
QUELQUES EXERCICES :
Approche de la division Trouver les restes Calcul mental 1 Calcul mental 2
C7: Triple, tiers, quadruple, quart...
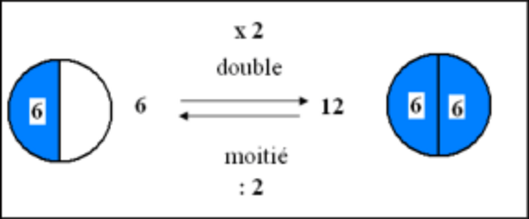
Relation entre double et moitié
Pour calculer le double d’un nombre, on le multiplie par 2.
Ex: le double de 6, c’est 6 x 2 =12.
Pour trouver la moitié d’un nombre on le divise par 2
Exemple: la moitié de 12, c’est 12 : 2 = 6
On remarque la relation entre doubles et moitiés .
Rapport entre le triple et le tiers
Pour calculer le triple d’un nombre, on le multiplie par 3.
Ex: le triple de 6, c’est 6 x 3 =18.
Pour trouver le tiers d’un nombre on le divise par 3.
Exemple: le tiers de 18, c’est 18 : 3 = 6.
On observe le lien qui existe entre le triple et le tiers.
Lien entre le quadruple et le quart
Pour calculer le quadruple d’un nombre, on le multiplie par 4.
Ex: le quadruple de 6, c’est 6 x 4 = 24.
Pour trouver le quart d’un nombre, on le divise par 4.
Exemple: le quart de 24, c’est 24 : 4 = 6.
On a bien une relation entre le quadruple et le quart.
C9: Somme et différence de deux décimaux
Poser les additions correctement
Poser des soustractions correctement
Effectuer une soustraction posée
Compléter une soustraction posée
C10: Multiplier ou diviser un nombre par 10, 100, 1000...
Multiplier un décimal par 10, 100 ou 1000 (facile)
Multiplier un décimal par 10, 100 ou 1000 (facile)
Multiplier un décimal par 10, 100 ou 1000 (difficile)
Multiplier un décimal par 10, 100 ou 1000 (difficile)
Diviser un décimal par 10, 100 ou 1000 (facile)
Diviser un décimal par 10, 100 ou 1000 (facile)
Diviser un décimal par 10, 100 ou 1000 (difficile)
Diviser un décimal par 10, 100 ou 1000 (difficile)
C11: Multiplier un décimal par un nombre entier
Exercice 1 Exercice 2 Exercice 3
C12: Multiplier un décimal par un nombre décimal
PB1: La proportionnalité
Petits problèmes Trouver le coefficient Proportionnalité ou pas? Problèmes et tableaux Sur un tableau
C13: La division posée (3): quotient décimal
Rappel de la technique à ' 1 chiffre,quotient entier':
225:8=?

Etape 1: Je cherche le nombre de chiffres au quotient:
J'encadre le dividende(ici 225 ) entre des multiples du diviseur(ici:8) terminés par des zéros.
8 x 10 <225< 8x 100
Le quotient entier est donc compris entre 10 et 100 => 2 chiffres au quotient.Etape 2: Je partage les centaines
2 est inférieur à 8 , donc je transforme les centaines en dizaines .
Je prends 2 chiffres pour commencer le partage.
En 22 combien de fois 8? 2 fois( 2x8=16), reste 6.
On écrit 2 au quotient et 6 sous le 2.Etape 3: Je partage les unités
On abaisse le 5. En 65 combien de fois 8? 8 fois,reste 1
On écrit 8 au quotient et 1 sous le 5 des unités.
La division est terminée dans le cadre d'un quotient entier.
Nous avons abaissé tous les chiffres du dividende et le quotient comporte bien 2 chiffres.Il ne me reste plus qu'à faire la preuve : 225=( 28 X 8)+1
QUOTIENT DECIMAL:
a) Au dixième près (1 chiffre après la virgule).

Il reste 1 unité . Je convertis le reste en dixièmes en écrivant un zéro à sa droite et je place une virgule au quotient.
En 10 combien de fois 8? 1 fois; il reste 2 dixièmes.
225 = (28,1x 8) +0,2
b) Au centième près (2 chiffres après la virgule).

Il reste 2 dixièmes . Je convertis le reste en centièmes en écrivant un zéro à sa droite et je poursuis la division.
En 20 combien de fois 8? 2 fois; il reste 4 centièmes.
225 = (28,12 x 8) +0,04
c) Au millième près ( 3 chiffres après la virgule).

Il reste 4 centièmes . Je convertis le reste en millièmes en écrivant un zéro à sa droite et je poursuis la division.En 40 combien de fois 8? 5 fois; il reste 0 millième.
225 = 28,125 x 8
Ici, le quotient est exact au millième près, mais il aurait pu être approché.
Dans ce cas, on ajouterait le reste en millièmes lors de la preuve, comme en a) et en b).
Pour les divisions avec un diviseur à plusieurs chiffres on procède selon la même démarche en convertissant les unités en dixièmes, centièmes ou millièmes selon la précision demandée.